1. 三角化(耳切法)
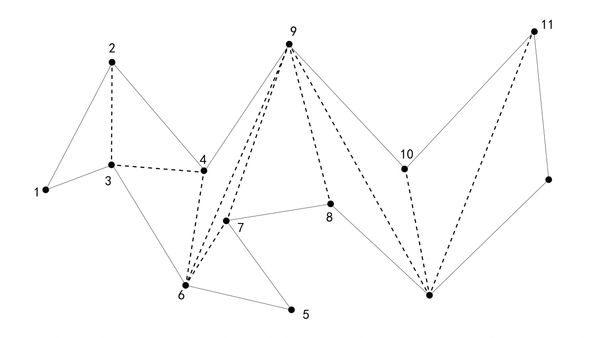
耳切算法
耳切法（Ear Clipping Method），是计算机图形学中用于将简单多边形三角剖分（Triangulation）的一种经典算法。该方法的核心思想是：逐步从多边形中“剪”掉一个个耳朵（Ear）直到只剩下一个三角形。这是处理二维多边形网格化（meshing）和渲染的重要基础。
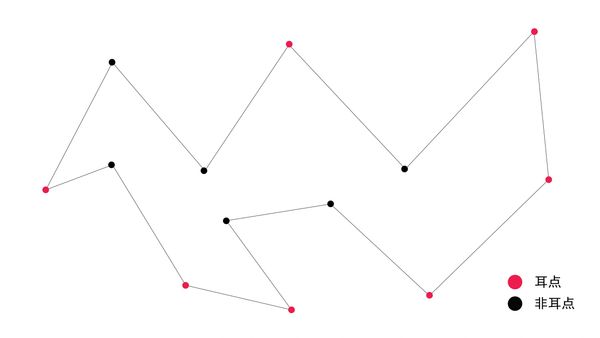
耳点的定义
对每个顶点 (v[i-1], v[i], v[i+1]) 检查是否构成一个耳朵：
- 是否是凸角（三角形内角 < 180°）；
- 该三角形内部是否包含其它顶点（用点在三角形内的测试判断）。
耳点判断步骤演示
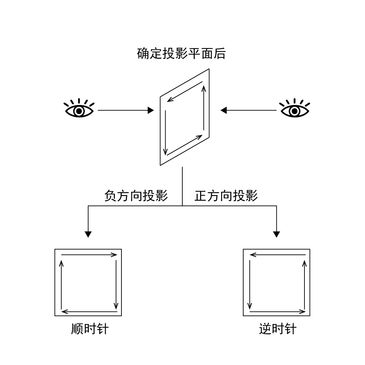
1. 确定投影的平面
3. 判断其他顶点是否位于三角形中
2. 判断v0是否为凸顶点
- 根据XYZ轴的差值决定往哪个平面坐标进行投影
- 要注意正方向或者负方向的投影，会影响顺逆时针
2. 判断v0是否为凸顶点
3. 判断其他顶点是否位于三角形中
2. 判断v0是否为凸顶点
确定顶点遍历顺序后，根据顺逆时针使用向量的叉积判断正负来决定是否为一个凸顶点
3. 判断其他顶点是否位于三角形中
3. 判断其他顶点是否位于三角形中
3. 判断其他顶点是否位于三角形中
使用重心坐标！(光栅化三角形)
2. 线性细分(Linear Subdivision)
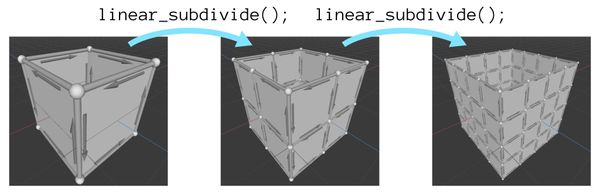
Linear细分
Linear细分是一种最基础的细分方法，其核心思想是：
不改变原始顶点的位置，只在边或面上添加新的顶点来细化网格。
步骤演示
1. 新增面重心顶点
1. 新增面重心顶点
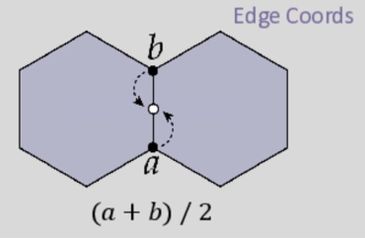
2. 新增边中点顶点
1. 新增面重心顶点
3. 保留原有顶点
3. 保留原有顶点
3. Catmull-Clark 细分
Catmull-Clark 细分
Catmull-Clark 细分是一种常用的平滑细分曲面算法（Subdivision Surface），广泛应用于建模和动画中，比如 Pixar、Maya、Blender 等都支持这种细分方式。
步骤演示
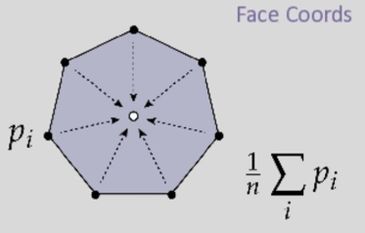
1. 新增面重心顶点
与Linear细分完全一致
2. 新增边中点顶点
除了边上的顶点作为权重，相邻的两个面也加入到插值
3. 计算新增顶点的位置
3. 计算新增顶点的位置
根据相邻的面重心边中点和原有顶点的位置插值计算新顶点的位置
4. Loop 细分(Loop是人名)
Loop 细分
Loop 细分是一种专门用于三角形网格的平滑细分算法，由 Charles Loop 提出，常用于角色动画、建模、图形渲染等领域。基于三角面网格，通过引入新顶点并重新计算旧顶点位置，使网格逐步趋近于平滑的三角形细分曲面（类似于 B-spline 的效果）。
步骤演示
1. 网格表面细分
2. 计算新的边中点位置
2. 计算新的边中点位置
产生新的边中点，这里使用边分解和边反转更快更方便地生成三角形网格
2. 计算新的边中点位置
2. 计算新的边中点位置
2. 计算新的边中点位置
根据相邻的四个点，计算新的中点的位置
3. 计算旧顶点的位置
2. 计算新的边中点位置
3. 计算旧顶点的位置
根据相邻的旧顶点位置，计算细分后旧顶点的位置