算法简介
Bresenham 直线算法
Bresenham 算法是一种高效的整数型光栅显示线绘制方法。它避免了浮点计算，使用增量误差跟踪，并选择最近的像素来近似直线。它快速、准确，在计算机图形学中得到广泛应用。
步骤 1：将多种情况合并为一个
1. 确保 x1 > x0
1. 确保 x1 > x0
1. 确保 x1 > x0
首先，确保从左到右画线。如果 x0 > x1，则交换它们！这可以将 8 种情况转换为 4 种。
2. 确保 dy > 0
1. 确保 x1 > x0
1. 确保 x1 > x0
其次，确保 delta y (y1-y0)>0。如果 dy < 0，则 stepY = -1，dy = |dy|
3. 确定步进主轴
1. 确保 x1 > x0
3. 确定步进主轴
第三，确定我们步进过程的主要方向很重要。如果斜率> 1，则意味着我们应该沿着 y 轴前进。
步骤2：步进并刷新误差
How to decide which pixel to be rendered next step
该算法通过将误差项 (errX 或 errY) 与 0 进行比较来确定下一个像素。
- 初始像素决策基于斜率计算。
- 误差项 (errX 或 errY) 使用基于整数的计算迭代更新：
- 如果误差为正，则算法沿对角线移动。
- 否则，它会水平移动。
- 当 Y 轴为主方向时，适用相同的逻辑。
算法原理
包围盒:
边缘函数1
边缘函数1
在三角形光栅化中使用Bounding Box主要是为了提高效率，减少不必要的计算，增强GPU并行处理，以及优化剔除和裁剪。
边缘函数1
边缘函数1
边缘函数1
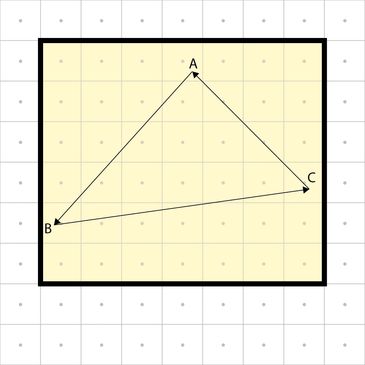
二维向量的叉积可以确定一个点是位于三角形边缘的左侧还是右侧。通过计算从该点到每个三角形顶点的向量的叉积，结果的符号可以定义该点是否位于三角形内。如果所有叉积的符号相同，则该点位于三角形内。
边缘函数2
边缘函数1
边缘函数2
二维向量的叉积既可以表示平行四边形的面积，也可以表示点到直线的垂直距离。
Dis(P, AB)越大，越接近C。而且这种方法可以显示出A,B,C的权重有多大
透视矫正
如何获得正确的颜色
由于透视投影（均匀划分），具有不同深度的三角形上的重心插值不是屏幕 XY 坐标的仿射函数
计算偏导
如何获得正确的导数
导数是根据像素之间的差异直接计算的，有前向和后向方法。需要注意的是，即使相邻像素不在三角形内，我们仍然需要使用重心坐标来计算它们数学意义上的值。